|
Markermenü (Elliptischer Bogen) |
|
|
Markermenü (Elliptischer Bogen) |
|
Im Markermenü des Elliptischen Bogens finden Sie alle Befehle zur direkten Modifikation des angewählten Bogens.
| ▪ | Um das Markermenü des Elliptischen Bogens aufzurufen, klicken Sie mit der linken Maustaste auf einen bereits gezeichneten Elliptischen Bogen im Grundriss Fenster oder in einer 3D Ansicht |
Je nach Klickpunkt stehen verschiedene Befehle zur Verfügung:
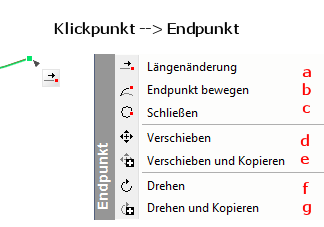
| a | Die Länge des Elliptischen Bogens kann entweder manuell oder mit Wert eingabe geändert werden |
| b | Mit diesem Befehl kann der Endpunkt in eine beliebige Richtung bewegt werden |
(der Elliptische Bogen dreht sich mit der klickrichtung mit)
| c | Schließt mann einen Elliptischen Bogen wird dieser automatisch zur Ellipse und kann als solche weiterbearbeitet werden |
| d | Hier wird der gesammte Elliptische Bogen verschoben |
| e | Anstatt den Elliptischen Bogen nur zu verschieben wird er an den neu definierten Ort kopiert |
| f | Bevor mann den Elliptischen Bogen drehen kann muss zuerst eine Hilfslinie erzeugt werden |
| g | Wie bei dem Befehl Drehen muss auch hier eine Hilfslinie erzeugt werden |
Der ausgewählte Elliptische Bogen bleibt jedoch auf seinem Platz und wird zu dem angegeben Drehpunkt kopiert
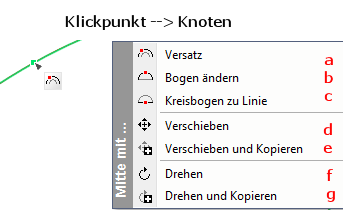
| a | Versetzt die Kontur des Elliptischen Bogens |
| b | Der Bogen kann in jede Richtung geändert werden |
| c | Aus dem Elliptischen Bogen wird eine Linie |
| d | Hier wird der gesammte Elliptische Bogen verschoben |
| e | Anstatt den Elliptischen Bogen nur zu verschieben wird er an den neu definierten Ort kopiert |
| f | Bevor mann den Elliptischen Bogen drehen kann muss zuerst eine Hilfslinie erzeugt werden |
| g | Wie bei dem Befehl Drehen muss auch hier eine Hilfslinie erzeugt werden |
Der ausgewählte Elliptischen Bogen bleibt jedoch auf seinem Platz und wird zu dem angegeben Drehpunkt kopiert
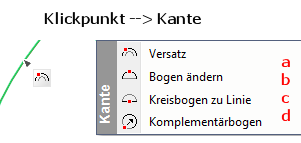
| a | Der Elliptische Bogen wird versetzt |
| b | Der Bogen kann in jede Richtung geändert werden |
| c | Aus dem Elliptische Bogen wird eine Linie |
| d | Hier wird der Teil angezeigt, der dem Elliptischen Bogen fehlt um eine Elipse zu werden |
Verwandte Themen |
